Chapter 2 信息的表示和处理

学习目标¶

理解计算机系统的复杂与和理论抽象描述的不同
理解内存中数据的保存形式，以及这种方式的好处以及限制
注意避开一些常见的关于计算机的迷思
区别整型和浮点数的表达机制，并理解为什么会有这种差异
简单理解溢出出现的条件

Part 1：比特¶

这一讲的主要内容 —— 比特(bit)。

研究问题有两种方法，一种是自顶向下，另一种是自底向上。对于设计来说，很多时候是自顶向下的，从一个整体想法出发，然后慢慢细化；而在学习化学的时候，往往是自底向上的，比方说先去了解组成元素的基本粒子，然后在这些粒子的基础上进行更加抽象的研究。从这个角度看，学习计算机系统，自底向上可能是一个好的方向。

在计算机中，我们看到的一切，归根到底，都是比特，每个比特不是 0 就是 1。计算机就是通过对比特进行不同方式的编码和描述，来完成执行不同的任务。那么问题来了，为什么是比特而不是其他呢？这就要从模拟电路讲起，一言以蔽之就是，比特这种描述方式很好存储，并且在有噪声或者传输不那么准确的情况下，也能保持比较高的可靠度（电压值有一定的容错范围）。

在这样的物理基础上，计算机就是一个二进制系统，我们通过下面这个表格来把二进制、十进制和十六进制一一对应起来，这三种数字表示形式在今后的学习过程中会反复出现，可以把这个表格当做九九乘法表来看：

十六进制	十进制	二进制	十六进制	十进制	二进制
0	0	0000	8	8	1000
1	1	0001	9	9	1001
2	2	0010	A	10	1010
3	3	0011	B	11	1011
4	4	0100	C	12	1100
5	5	0101	D	13	1101
6	6	0110	E	14	1110
7	7	0111	F	15	1111

正如加减乘除，关于比特的基本逻辑运算==也有四种，可以==看==做是布尔代数的子集。对于 0 和 1 来说，是这样的：

与 And：A=1 且 B=1 时，A&B = 1
或 Or：A=1 或 B=1 时，A|B = 1
非 Not：A=1 时，~A=0；A=0 时，~A=1
异或 Exclusive-Or(Xor)：A=1 或 B=1 时，A^B = 1；A=1 且 B=1 时，A^B = 0

对应与集合运算则是交集、并集、差集和补集，假设集合 A 是 {0, 3, 5, 6}，集合 B 是 {0, 2, 4, 6}，全集为 {0, 1, 2, 3, 4, 5, 6, 7}那么：

& 交集 Intersection {0, 6}
| 并集 Union {0, 2, 3, 4, 5, 6}
^ 差集 Symmetric difference {2, 3, 4, 5}
~ 补集 Complement {1, 3, 5, 7}

有了这些知识，我们就可以来具体看看不同类型的数据在计算机中是如何存储和进行运算的了。

Part2：整型 Integer¶

C 语言之所以效率高，很大程度上是因为抽象程度较低，很多关键字和计算机系统中的概念是一一对应的。比方说 signed 和 unsigned，就表示有符号数和无符号数。假设字长(word size)为 w，那么==二进制向十进制的转换==分别是：

无符号数：$B2U(X)=\sum_{i=0}^{w-1}x_i·2^i$
有符号数： $B2T(X)=-x_{w-1}·2^{w-1}+\sum_{i=0}^{w-2}x_i·2^i$

==有符号数和无符号数的区别主要在于有没有最高位的符号位，以及由此带来的计算方式的不同。符号位中，0 表示非负数，1 表示负数。==具体的表示方法如下

十进制	十六进制	二进制
15213	3B 6D	00111011 01101101
-15213	C4 93	11000100 10010011

对于==二进制数字来说，还有两种常用操作：左移和右移==。左移比较简单，在右边补 0 即可。右移的话有两种类型，一种是==逻辑右移（左边补 0），另一种是算术右移（左边补符号位）==。为什么会有这两种，因为对应无符号数和有符号数的运算，有符号数的最高位（最左边）是符号位在负数的时候需要进行算术右移

Part3：整型表示的特点¶

接下来我们看看这种表示形式的特点，以及溢出的集中情况，假设字长为 w，定义如下的常量：

UMin = 0 即 000…0
UMax = $2^w-1$ 即 111…1
TMin = $-2^{w-1}$ 即 100…0
TMax = $2^{w-1}-1$ 即 011…1
Minus 1 即 111…1

这里的 U 表示无符号数，T 表示补码(Two’s Complement)，对于字长为 16 的情况来说，我们有：

||Decimal|Hex|Binary| |---|---|---|---| |UMax|65535|FF FF|11111111 11111111| |TMax|32767|7F FF|01111111 11111111| |TMin|-32768|80 00|10000000 00000000| |-1|-1|FF FF|11111111 11111111| |0|0|00 00|00000000 00000000|

对于不同的 word size，数值也会有很大的变化

w	8	16	32	64
UMax	255	65,535	4,294,967,295	18,446,744,073,709,551,615
TMax	127	32,767	2,147,483,647	9,223,372,036,854,775,807
TMin	-128	-32,768	-2,147,483,648	-9223,372,036,854,775,808

观察可以得知==两个很重要的特性==

|TMin| = TMax + 1 (范围并不是对称的)
UMax = 2*TMax + 1

有符号数和无符号数在非负数的编码是一样的，每一个数字的编码是唯一的，这两者可以互换：

$U2B(x)=B2U^{-1}(x)$
$T2B(x)=B2T^{-1}(x)$

Part4：类型转换¶

我们在数轴上把有符号数和无符号数画出来的话，就能很清晰的看出相对的关系：

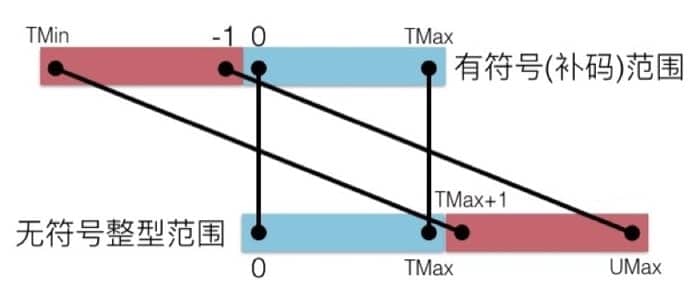
在==C 语言中，如果不加关键字限制，默认的整型是有符号的。如果想要无符号数的话，需要在数字后面加 U==，例如下面的代码段


1 2	int a_signed_number = -15213; unsigned int a_unsigned_number = 15213U;

在==进行有符号和无符号数的互相转换==时：

具体每一个字节的值不会改变，改变的是计算机解释当前值的方式
如果一个表达式既包含有符号数也包含无符号数，那么会被隐式转换成无符号数进行比较

下面用字长 w = 32 为例，来进行说明，注意这里的每个表达式都是成立的，其中 TMin = -2,147,483,648, TMax = 2,147,483,647

表达式	比较对象
0 == 0U	无符号数
-1 < 0	有符号数
-1 > 0U	无符号数
2147483647 > (-2147483647-1)	有符号数
2147483647U < (-2147483647-1)	无符号数
-1 > -2	有符号数
(unsigned)-1 > -2	无符号数
2147483647 < 2147483648U	无符号数
2147483647 > (int)2147483648U	有符号数

Part5：类型扩展与截取¶

具体需要分情况讨论，如：

扩展（例如从 short int 到 int），都可以得到预期的结果
- 无符号数：加 0
- 有符号数：加符号位
截取（例如 unsigned 到 unsigned short），对于小的数字可以得到预期的结果
- 无符号数：mod 操作
- 有符号数：近似 mod 操作

举个例子


1 2 3 4	short int x = 15213; int ix = (int) x; short int y = -15213; int iy = (int) y;

C 语言会自动做符号拓展，把小的数据类型转换成大的，如下表所示

十进制	十六进制	二进制
x=15213	3B 6D	00111011 01101101
ix=15213	00 00 3B 6D	00000000 00000000 00111011 01101101
y=-15213	C4 93	11000100 10010011
iy=-15213	FF FF C4 93	11111111 11111111 11000100 10010011

Part6：运算与溢出¶

**无论是无符号数还是有符号数，一旦用来表示数值的最高位发生了进位，超出了表达形式或者改变了符号位，就会发生溢出。

（1）加法：¶

对于==无符号数加法，如果两个 w 位的数字相加，结果是 w+1 位的话，那么就会丢弃掉最高位，实际上是做了一个 mod 操作==（公式为 $s=UAdd_w(u,v)=u+v \; mod \; 2^w$）

假设 w=3，那么能够表达的数字范围是 000~111(0~7)（括号内为二进制对应的十进制数值，后同），那么如果一个表达式是 110+111(6+7)，原本应该等于 1101(13)，但是由于 w=3，所以最终的结果是 101(5)，也就是发生了溢出，两个无符号数相加，有可能反而变『小』。

对于==有符号的加法(Two’s Complement Addition)，操作过程和无符号加法一样，只是解释的时候会有不同，因此会得到正溢出(positive overflow)和负溢出(negative overflow)两种==。正溢出就是数值太大把原来为 0 的符号位修改成了 1，反而成了负数；负溢出是数值太小，把原来为 1 的符号位修改成了 0，反而成了正数。

还是用刚才 w=3 作为例子，能够表达的数字范围是 100~011(-4~3)，如果一个表达式是 011+010(3+2)，理论上应该等于 5，但是相加之后变成了 101(-3)，也就是发生了正溢出。如果一个表达式是 100+101(-4+(-3))，理论上应该等于 -7，但是相加后进位截取变成了 001(1)，也就是发生了负溢出。

（2）乘法：¶

对于乘法来说，值的范围会大很多，这里分情况讨论一下，==假设两个乘数是 x,y 并且都是 w 位==的：

无符号数：至多 2w 位
- 范围 $0 \le x \times y \le (2^w-1)^2 = 2^{2w}-2^{w+1}+1$
有符号数，最小的负数：至多 2w - 1 位
- 范围 $x \times y \ge (-2^{w-1})\times(2^{w-1}-1)=-2^{2w-2}+2^{w-1}$
有符号数，最大的正数：至多 2w 位，只有 $(TMin_w)^2$ 一种情况
- 范围 $x \times y \le (-2^{w-1})^2=2^{2w-2}$

如果需要保证精度，就需要用软件来实现了。==另外，计算的无符号乘法的时候，会忽略最高的 w 位，==相当于 $UMult_w(u,v)=u·v\;mod\;2^w$

Part7：浮点数 Float¶

浮点数可以用一个统一的公式来表达：

例如

可以看到==除以二就相当于右移==，并==且可以横跨小数点==。注意 $0.111…_2$ 非常接近于 1，因为

通常用 $1.0-\epsilon$ 来表示这个值。

细心的同学就会发现，这种表达方式其实是比较明显的限制的，比如说，只有形为 $\frac{x}{2^k}$ 的小数部分可以被精确表示，其他的数字会变成循环的小数，例如：$\frac{1}{3}=0.0101010101[01]…_2$。

除此之外，另一个问题在于，如果给定了 w 个比特，能够表达的数字其实是有限的，具体的原因会在后面详细解释。

Part8：IEEE 浮点数标准¶

IEEE 的浮点数标准更多是从数值角度来建立的，对于舍入，上溢出和下溢出都有比较统一的处理方法。但与此同时也给硬件优化带来了比较大的困难。因为和平时使用的数制也有一定差异，从理解的角度来看不够直观，但是好在主流的 CPU 都支持浮点数，所以我们不必过多涉及这方面的细节。

在 IEEE 标准中，我们用下面的公式来表达浮点数：

其中 s 是符号位，决定正负；M 通常是一个值在 [1.0, 2.0) 的小数；E 是次方数。

具体编码时结构如下，这里用单精度、双精度和扩展精度为例：

其中 s 对应着符号位，exp 对应着 E（注意，不一定等于 E，因为位数限制表达能力有限），frac 对应着 M（注意，不一定等于 M，因为位数限制表达能力有限）。不同的位数就代表了不同的表示能力，也就是单精度，双精度，扩展精度的来源。

(1) 规范化值(Normalized Values)

在 $exp \ne 000…0$ 和 $exp \ne 111…1$ 时，表示的其实都是规范化的值，为什么说是规范化呢？这里只需要大概知道==因为实数轴上原来连续的值会被规范到有限的定值上==并==且这些定值之间的间距也是不一样的==，具体可以通过后面给出的例子来理解（所以现在不明白也不用担心）

再来回顾一下我们==计算浮点数的公式：==

这里的 ==E ==是一个偏移的值 $E=Exp-Bias$，其中

Exp: 是 exp 编码区域的无符号数值
Bias：值为 $2^{k-1} - 1$ 的偏移量，其中 k 是 exp 编码的位数，也就是说
- 单精度：127（Exp: 1…254, E: -126…127）
- 双精度：1023（Exp: 1…2046, E: -1022…1023）
- k: 由上述易见，对于给定精度的数字而言，是定值！

之所以需要采用一个偏移量，是为了保证 exp 编码只需要以无符号数来处理。

而对于 M，一定是以 1 开头的：也就是 $M=1.xxx…x_2$。其中 xxx 的部分就是 frac 的编码部分，当 frac=000.00 的时候值最小（$M=1.0$），当 frac=111。。。1 的时候值最大（$M=2.0-\epsilon$），也就是说==开头的 1 是『免费附送的』，并不需要实际的编码位==。

举个例子，float F = 15213.0;，那么

于是 frac 部分的值就是小数点后面的数值，而 Exp = E + Bias = 13 + 127 = 140 = $10001100_2$，于是编码出来的浮点数是这样的：


1 2	0 10001100 11011011011010000000000 s exp frac

（2）非规范化值(Denormalized Values)

当 $exp = 000…0$ 的时候，值是非规范化的，意思是，虽然实数轴上原来连续的值会被规范到有限的定值上，但是并些定值之间的间距也是一样的，具体可以通过后面给出的例子来理解（所以现在不明白也不用担心）

和前面不同的是

而且 $M=0.xxx…x_2$，不是以 1 开头了。

当 exp=000…0 且 frac = 000…0 时，表示 0，而且因为符号位的缘故，实际上是有 +0 和 -0 两种的。而在 exp=000..0 且 $frac \ne 000…0$ 时，数值是接近 0 的，并且间距是一致的

（3）特殊值

还有一种特殊情况，就是 $exp = 111…1$ 时，表示一些特殊值。

当 exp=111…1 且 frac = 000…0 时，表示 $\infty$，而且因为符号位的缘故，实际上是有 $+\infty$ 和 $-\infty$ 两种的。那些会溢出的操作就会用这个来表示，比如 $1.0/0.0=-1.0/0.0=+\infty\;,\;1.0/-0.0=-\infty$

而在 exp=111…1 且 $frac \ne 000…0$ 时，我们认为这不是一个数值（Not-a-Number，NaN），用来表示那些没办法确定的值，比如 $sqrt(-1),\infty-\infty,\infty\times 0$

（4）实例学习

可能通过文字描述还是不够清晰，我们来看看上面各种情况对应到数轴中是怎么样的：

接下来举一个实际的例子，我们采用 1 位符号位，4 位 exp 位，3 位 frac 位，因此对应的 bias 为 7。回顾一下几个重要公式：

==对于规范化数：$E=Exp-Bias$；对于非规范数：$E = 1 - Bias$，正数部分的数值为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

s exp frac E 值
------------------------------------------------------------------
0 0000 000 -6 0 # 这部分是非规范化数值，下一部分是规范化值
0 0000 001 -6 1/8 * 1/64 = 1/512 # 能表示的最接近零的值
0 0000 010 -6 2/8 * 1/64 = 2/512
...
0 0000 110 -6 6/8 * 1/64 = 6/512
0 0000 111 -6 7/8 * 1/64 = 7/512 # 能表示的最大非规范化值
------------------------------------------------------------------
0 0001 000 -6 8/8 * 1/64 = 8/512 # 能表示的最小规范化值
0 0001 001 -6 9/8 * 1/64 = 9/512
...
0 0110 110 -1 14/8 * 1/2 = 14/16
0 0110 111 -1 15/8 * 1/2 = 15/16 # 最接近且小于 1 的值
0 0111 000 0 8/8 * 1 = 1
0 0111 001 0 9/8 * 1 = 9/8 # 最接近且大于 1 的值
0 0111 010 0 10/8 * 1 = 10/8
...
0 1110 110 7 14/8 * 128 = 224
0 1110 111 7 15/8 * 128 = 240 # 能表示的最大规范化值
------------------------------------------------------------------
0 1111 000 n/a 无穷 # 特殊值

观察上表，我们可以发现如下一些比较有意思的规律：

在 exp=0000 时，也就是非规范化的情况，间距是一致的，都是 1/8
因为位数的限制，从零到一之间的数字只能以 1/8 为最小单位来表示，且相邻数字间间距一样
在规范化的部分，可以发现由于 exp 部分的不同，所以相邻数字间的间隔也是不同的，比方说最接近 1 的数字是 15/16 和 9/8，分别相差 1/16 和 1/8，这也是由于 IEEE 浮点数表示法的公式决定的

Part9：舍入¶

对于浮点数的加法和乘法来说，我们可以先计算出准确值，然后转换到合适的精度。在这个过程中，既可能会溢出，也可能需要舍入来满足 frac 的精度。

在二进制中，我们舍入到最近的偶数，即如果出现在中间的情况，舍入之后最右边的值要是偶数（取偶原则），对于十进制数，例子如下：（保留到百分位）


1 2 3 4 5	原数值舍入结果原因 2.8949999 2.89 不到一半，正常四舍五入 2.8950001 2.90 超过一半，正常四舍五入 2.8950000 2.90 ==刚好在一半==时，保证最后一位是偶数，所以向上舍入 2.8850000 2.88 ==刚好在一半==时，保证最后一位是偶数，所以向下舍入

对于二进制数也是类似的


1 2 3 4 5	十进制二进制舍入结果十进制原因 2 又 3/32 10.00011 10.00 2 不到一半，正常四舍五入 2 又 3/16 10.00110 10.01 2 又 1/4 超过一般，正常四舍五入 2 又 7/8 10.11100 11.00 3 刚好在一半时，保证最后一位是偶数，所以向上舍入 2 又 5/8 10.10100 10.10 2 又 1/2 刚好在一半时，保证最后一位是偶数，所以向下舍入

Part10：浮点数加法¶

$\((-1)^{s_1}\; M_1 \; 2^{E_1} + (-1)^{s_2}\; M_2 \; 2^{E_2}$\) 这里假设 $E_1 > E_2$，结果是 $(-1)^{s}\; M \; 2^{E}$ ，其中 $s = s_1 \land s_2, M = M_1 + M_2, E = E_1$

如果 M 大于等于 2，那么把 M 右移，并增加 E 的值
如果 M 小于 1，把 M 左移 k 位，E 减少 k
如果 E 超出了可以表示的范围，溢出
把 M 舍入到 frac 的精度

基本性质

相加可能产生 infinity 或者 NaN
满足交换律
==不满足结合律（因为舍入会造成精度损失，如 (3.14+1e10)-1e10=0，但 3.14+(1e10-1e10)=3.14）
加上 0 等于原来的数
除了 infinity 和 NaN，每个元素都有对应的倒数（拥有加法逆元）
除了 infinity 和 NaN，满足单调性，即 $a\ge b \to a+c \ge b+c$

Part11：浮点数乘法¶

\[(-1)^{s_1}\; M_1 \; 2^{E_1} \times (-1)^{s_2}\; M_2 \; 2^{E_2}\]

结果是 $(-1)^{s}\; M \; 2^{E}$，其中 $ s= s_1 \land s_2, M = M_1 \times M_2, E = E_1 + E_2$

如果 M 大于等于 2，那么把 M 右移，并增加 E 的值。
如果 E 超出了可以表示的范围，溢出
把 M 舍入到 frac 的精度

基本性质

相乘可能产生 infinity 或者 NaN
满足交换律
不满足结合律（因为舍入会造成精度损失）
乘以 1 等于原来的数
不满足分配率 1e20*(1e20-1e20)=0.0 但 1e20*1e20-1e20*1e20=NaN
除了 infinity 和 NaN，满足单调性，即 $a\ge b \to a\times c \ge a\times b$

Part12：数据在内存中的形式¶

后续章节会有关于内存的详细介绍，这里我们只要知道不同数据类型所占据的字节数，以及大端-小端规则即可。

操作系统会给每个进程提供私有的虚拟内存地址空间，一个进程可以访问自己的数据，但是不能访问别人的数据。在虚拟内存中地址是连续的，对应物理内存则不一定，根据字长的不同，有不同的间隔，如下图所示

然后我们来看看常见数据类型所需要的字节数：

数据类型	32 位	64 位	x86-64
char	1	1	1
short	2	2	2
int	4	4	4
long	4	8	8
float	4	4	4
double	8	8	8
long double	-	-	10/16
指针	4	8	8

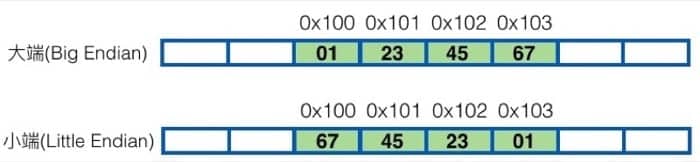
数据具体的排列也有两种方式：大端(Big Endian)与小端(Little Endian)，区别在于高位地址的位置。Internet 数据采用大端规则，而我们常见的 x86 或 ARM 处理器都采用小端规则。

举个例子，假如变量 x 是 4 字节，值为 0x01234567。用 &x 索引的地址是 0x100，那么大端和小端的表示形式是

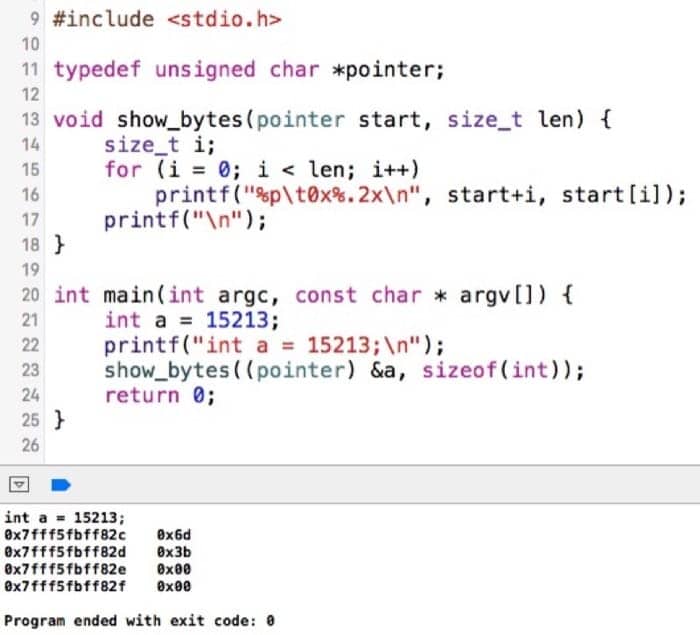
如何检查数据的表示呢，可以用下面的代码


1 2 3 4 5 6 7 8	typedef unsigned char *pointer; void show_bytes(pointer start, size_t len)

这里 %p 用来输出指针，%x 用来输出 16 进制数据。执行可用：


1 2 3	int a = 15213; printf("int a = 15213;\n"); show_bytes((pointer) &a, sizeof(int));

在我的电脑上，测试如下：

csapp12